在计算机科学中，二叉树是一种常见的数据结构，其每个节点最多有两个子节点（通常称为左子节点和右子节点），二叉树模型定义是理解和应用二叉树的基础，本文将详细介绍二叉树的定义、特性、类型以及其在不同领域的应用。

二叉树的定义

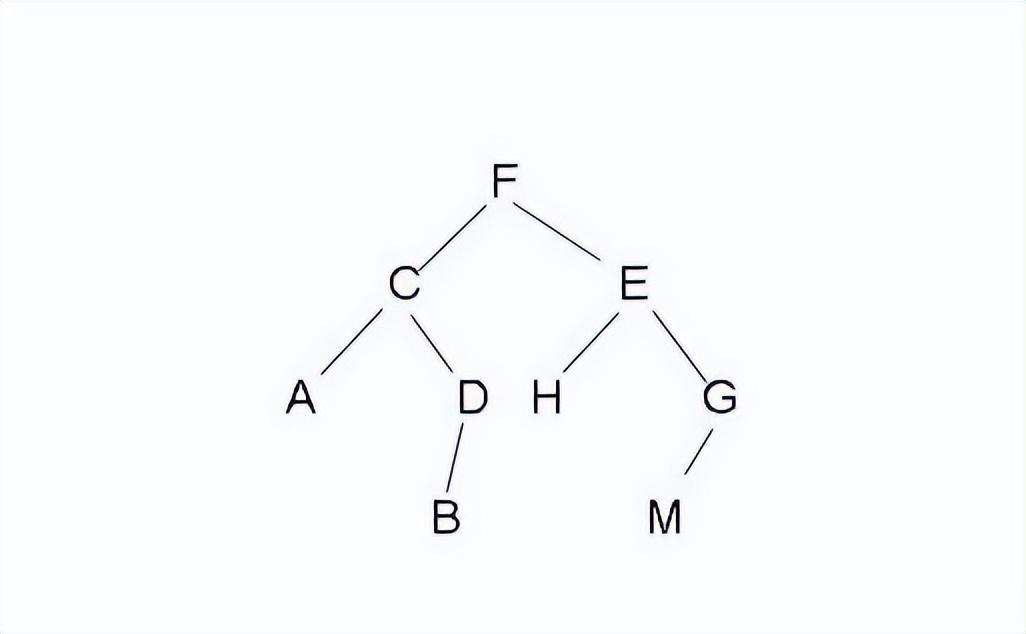
二叉树是一种树形结构，其中每个节点最多有两个子节点，节点的子节点被称为左子节点和右子节点，二叉树的根节点是没有父节点的节点，其余节点或者是叶子节点（没有子节点），或者是内部节点（拥有两个子节点），这种结构使得二叉树在数据存储和检索方面具有很高的效率。

二叉树的特性

1、递归性：二叉树的构建具有递归性质，即根节点包含左右子树，而左子树和右子树本身也是二叉树，这种递归性质使得二叉树在算法设计和实现中具有独特的优势。

2、层次结构：二叉树的节点按照一定的层次排列，根节点位于第0层，根节点的直接子节点位于第1层，以此类推，这种层次结构使得二叉树在数据存储和检索过程中能够快速定位到特定节点。

二叉树的类型

根据节点的性质，二叉树可以分为多种类型，常见的二叉树类型包括：

1、完全二叉树：除了最后一层外，其他层的节点数均达到最大，且最后一层的节点尽可能集中在左侧，完全二叉树在堆排序等算法中具有广泛应用。

2、满二叉树：所有节点都有两个子节点，满二叉树在二叉搜索树等数据结构中有重要应用。

3、二叉搜索树（BST）：一种特殊的二叉树，其任何节点的值都大于其左子树中任意节点的值且小于其右子树中任意节点的值，二叉搜索树在数据查找、插入和删除等操作中具有高效性能。

二叉树模型的应用

二叉树模型在计算机科学、数学、计算机科学等领域有广泛的应用，以下是几个典型的应用场景：

1、数据压缩：在数据压缩算法中，如哈夫曼编码，使用哈夫曼树（一种特殊的二叉树）来表示数据的编码，从而提高数据压缩效率。

2、编译器设计：编译器在处理源代码时，利用语法分析树（一种二叉树或三叉树）来解析源代码，从而实现代码编译过程。

3、搜索与排序：在数据搜索和排序过程中，如二分搜索树（BST）和AVL树等平衡二叉搜索树，利用二叉搜索树的特性提高搜索和排序效率。

4、操作系统：操作系统的文件系统可以使用二叉树来管理文件和目录，文件路径可以表示为从根节点到叶子节点的路径，从而快速定位文件。

5、机器学习：在机器学习中，决策树和神经网络等模型涉及复杂的二叉树结构，这些模型在处理分类和回归问题时具有很高的性能。

二叉树作为一种基本的数据结构，在计算机科学、数学等领域具有广泛的应用，本文介绍了二叉树的定义、特性、类型以及应用场景，理解二叉树的定义和特性对于掌握数据结构、算法设计和软件开发具有重要意义，在实际应用中，根据具体需求选择合适的二叉树类型，如完全二叉树、满二叉树和二叉搜索树等，能够提高数据处理效率，随着计算机科学的不断发展，二叉树在机器学习等领域的应用将越来越广泛。